久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 已知函數(shù)與函數(shù)

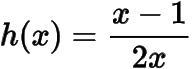
()的圖象有且只有一條公切線，求實(shí)數(shù)的值．

分析與解 法一 分離

由于函數(shù)的導(dǎo)函數(shù)分別為

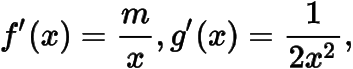
設(shè)公切線與函數(shù)與函數(shù)的圖象分別相切于與

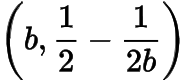
，則

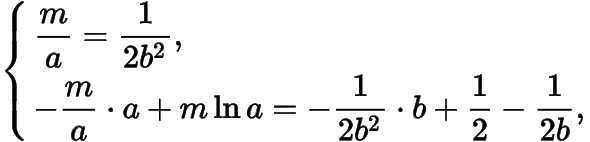
從而

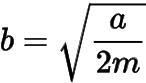
，且

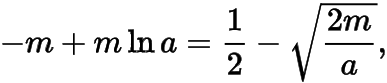
即

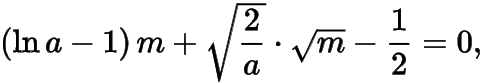
于是

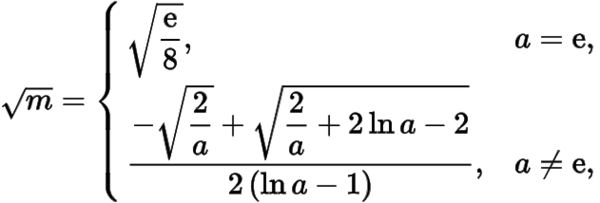
即

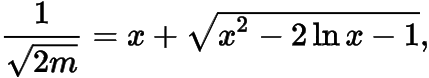
其中

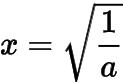
．記上述等式右邊為，對求導(dǎo)得

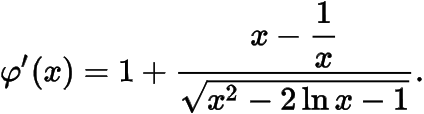
可以證明當(dāng)時(shí)，；當(dāng)時(shí)，（可以利用與

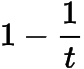
的大小關(guān)系得到與

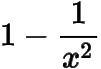
的大小關(guān)系，從而得到結(jié)論）．

從而有在上單調(diào)遞減，在上單調(diào)遞增．當(dāng)時(shí)，取得最小值．因此當(dāng)

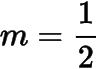
時(shí)，符合題意．

綜上所述，實(shí)數(shù)的值為，對應(yīng)的公切線方程為

．

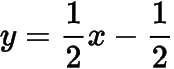
法二 不分離

在點(diǎn)處的切線為

而在點(diǎn)

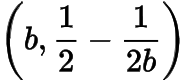
處的切線為

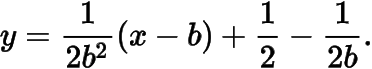
由這兩條切線重合知

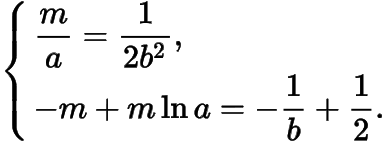
問題即當(dāng)在什么范圍內(nèi)時(shí)，關(guān)于的方程有唯一一組解．因?yàn)榕c的值一一對應(yīng)，如果在方程組中消去，得到

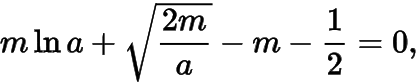
此方程組對有唯一解，不好計(jì)算；

如果在方程組中消去得到

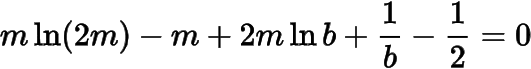
對有唯一解，記左邊為，則有

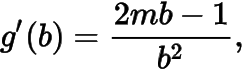
方程組有解時(shí)有，所以在

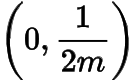
上單調(diào)遞減，在

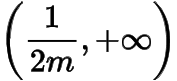
上單調(diào)遞增，所以

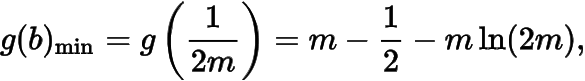
而當(dāng)與時(shí)，均有，所以當(dāng)且僅當(dāng)這個(gè)最小值等于零時(shí)方程有唯一解．

最后解方程

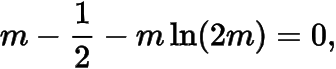
顯然

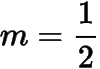
是它的解，考慮

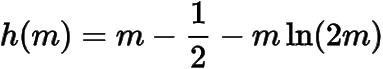
，有，所以在

上單調(diào)遞增，在

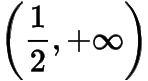
上單調(diào)遞減，所以是的唯一解，所以