久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 級數(shù)不等式的證明題是一種常見的問題，利用導(dǎo)數(shù)證明級數(shù)不等式更是一種典型問題，有好多學(xué)生，甚至老師對這類問題很畏懼，其實只要抓住這類問題的本質(zhì)進行合理的處理，問題就可以迎刃而解了．要解決這類問題，通常需要分析通項，得到一個不等關(guān)系，然后累加即可得到要證明的式子．例如：要證明

，只要證明，再注意一下時的式子即可．

例 已知函數(shù)，

，．

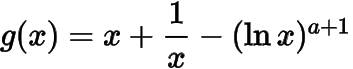
（1）若在定義域內(nèi)恒成立，求的取值范圍；

（2）當取（1）中的最大值時，求函數(shù)的最小值；

（3）證明不等式

．

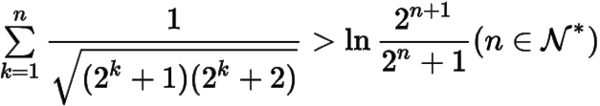
——提問者：888888中山大學(xué) 2016-09-19 00:23

分析本題的第一、第二問都是基礎(chǔ)題，考查利用導(dǎo)數(shù)研究函數(shù)的最值問題，難點顯然在第三問．事實上，前兩問都是為第三問做準備的，下面來看一下具體的解析過程．

解（解答者：df0817）

（1）由題意有在恒成立，令則

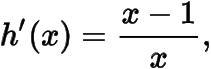
在單調(diào)遞減，在單調(diào)遞增，所以于是．

（2）由題意

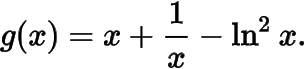
求導(dǎo)

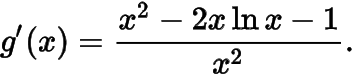
令則所以在上單調(diào)遞增，注意到所以在單調(diào)遞減，在單調(diào)遞增，所以即的最小值為．

（3）級數(shù)不等式的通項為

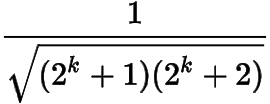
，分析通項

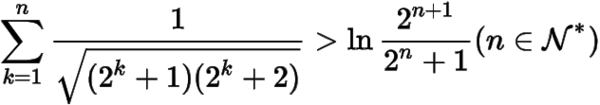
只需證明

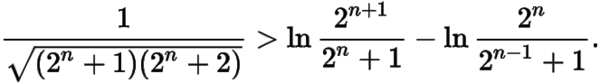
即

這個式子的證明可以借助第二問中的結(jié)論，由（2）可得

即

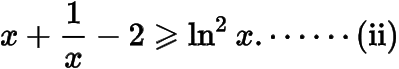
分析(i)(ii)兩式可設(shè)

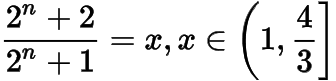
則

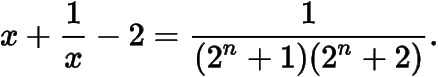
于是(i)式成立，所以得證．

注解決本題時，分析通項是關(guān)鍵．在解題時，可以把已知的函數(shù)不等式和要證的通項進行對照，必要時可以通過合理的變形，把它們聯(lián)系起來．

練習(xí)

1．已知函數(shù)．

（1）若函數(shù)在其定義域上為增函數(shù)，求的取值范圍；

（2）設(shè)

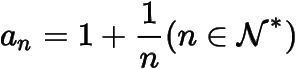
，求證：

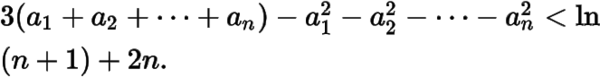
——提問者：weilew 2016-09-19 09:42

2．已知函數(shù)

，且在

處的切線方程為．

（1）求 的解析式；

（2）證明：當時，恒有；

（3）證明：若，且

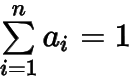
，則

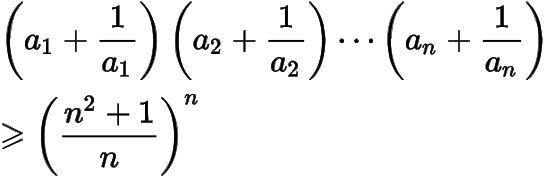
——提問者：Imagine 2016-09-04 11:30

3．求證：當且時，

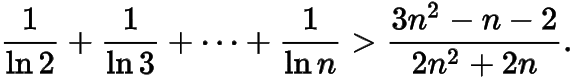
——提問者：湫兮如風(fēng)凄兮如雨 2016-09-15 09:04

答案

1．（1）；（2）略

2．（1）

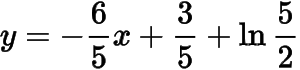
；（2）（3）略

3．略

備注：若要查閱詳細的解答過程，請在光子問答APP中搜索用戶名，查看用戶提問的問題，找到對應(yīng)時間所發(fā)的題即可．