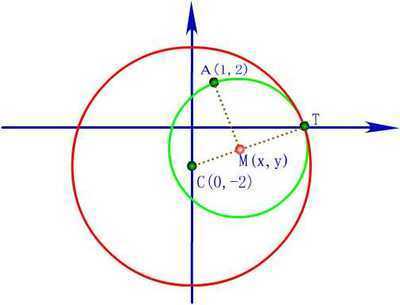
研究直線與圓錐曲線的位置關系時,一般轉化為研究其直線方程與圓錐方程組成的方程組解的個數,但對于選擇、填空題也可以利用幾何條件,用數形結合的方法求解.
1.直線與圓錐曲線的位置關系,主要涉及弦長、弦中點、對稱、參數的取值范圍、求曲線方程等問題.解題中要充分重視根與系數的關系和判別式的應用.
2.當直線與圓錐曲線相交時:涉及弦長問題,常用“根與系數的關系”設而不求計算弦長(即應用弦長公式);涉及弦的中點問題,常用“點差法”設而不求,將弦所在直線的斜率、弦的中點坐標聯系起來,相互轉化.同時還應充分挖掘題目中的隱含條件,尋找量與量間的關系靈活轉化,往往就能事半功倍.解題的主要規律可以概括為“聯立方程求交點,韋達定理求弦長,根的分布找范圍,曲線定義不能忘”.
一、直線與圓錐曲線的位置關系
判定直線與圓錐曲線的位置關系時,通常是將直線方程與曲線方程聯立,消去變量y(或x)得關于變量x(或y)的方程:ax2+bx+c=0(或ay2+by+c=0).
若a≠0,可考慮一元二次方程的判別式Δ,有:
Δ>0?直線與圓錐曲線相交;
Δ=0?直線與圓錐曲線相切;
Δ<0?直線與圓錐曲線相離.
若a=0且b≠0,則直線與圓錐曲線相交,且有一個交點.
典型例題1:


二、圓錐曲線的弦長問題
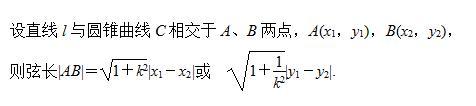
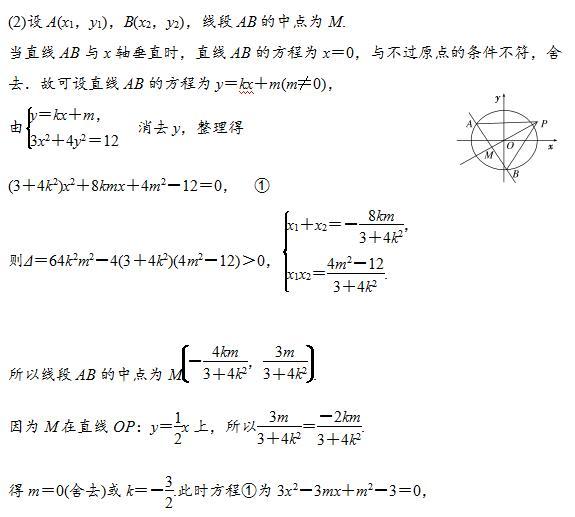
典型例題2:


1、解決圓錐曲線的最值與范圍問題常見的解法有兩種:幾何法和代數法.
(1)、若題目的條件和結論能明顯體現幾何特征和意義,則考慮利用圖形性質來解決,這就是幾何法;
(2)、若題目的條件和結論能體現一種明確的函數關系,則可首先建立起目標函數,再求這個函數的最值,這就是代數法.
2、在利用代數法解決最值與范圍問題時常從以下五個方面考慮:
(1)、利用判別式來構造不等關系,從而確定參數的取值范圍;
(2)、利用已知參數的范圍,求新參數的范圍,解這類問題的核心是在兩個參數之間建立等量關系;
(3)、利用隱含或已知的不等關系建立不等式,從而求出參數的取值范圍;
(4)、利用基本不等式求出參數的取值范圍;
(5)、利用函數的值域的求法,確定參數的取值范圍.
典型例題3:


1、求定值問題常見的方法有兩種
(1)、從特殊入手,求出表達式,再證明這個值與變量無關;
(2)、直接推理、計算,并在計算推理的過程中消去變量,從而得到定值.
2、定點的探索與證明問題
(1)、探索直線過定點時,可設出直線方程為y=kx+b,然后利用條件建立b、k等量關系進行消元,借助于直線系方程找出定點;
(2)、從特殊情況入手,先探求定點,再證明一般情況.
典型例題4:

今天的內容就先和大家分享到這了,希望大家喜歡!
