答案.
分析與解注意到是函數的零點,而不是函數的零點,于是問題等價于函數
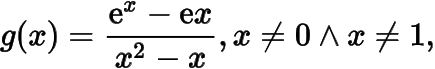
的圖象與直線
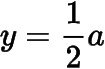
有兩個公共點.函數的導函數
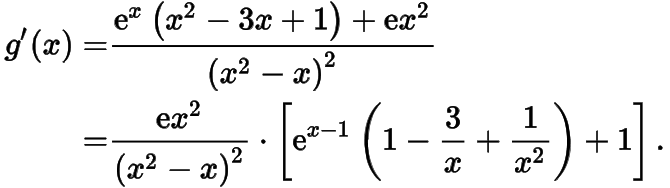
設函數
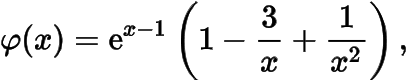
則其導函數

于是的最小值為.這樣我們就得到了在,,上均單調遞增.顯然在上,;在上;在上.于是當時,函數的圖象與直線
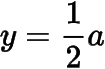
至多只有一個公共點,不符合題意.
接下我們證明當時,函數的圖象與直線
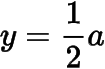
恰好有兩個公共點,它們的橫坐標分別位于區間和.證明的關鍵在于在每個區間上,對于任意給定的正數,都存在比大的函數值以及比小的函數值.
在區間上,由于
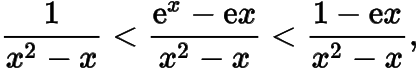
而在區間上,函數

可以取到比大的函數值,而函數
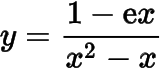
可以取到比小的函數值;
在區間上,一方面由積分兩次可得
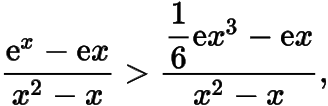
而在區間上,函數
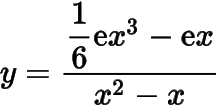
可以取到比大的函數值;另一方面,在區間上,有

而在區間上,函數
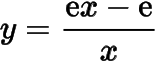
可以取到比小的函數值.
綜上,實數的取值范圍是.
注對在上進行積分得

再積分一次即可得到
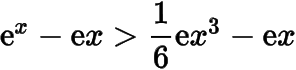
,也可以直接證明此不等式,但積分可以得到這個不等式的樣子,我們希望分子是一個三次函數.
另法對求導得從而有當時,,單調遞增,從而最多有兩個單調區間,不可能有三個不同的零點;
當時,先減后增,最小值為,而,所以一定有兩個零點,記為,且有.
而當時,可以取到正數;時,可以取到正數(嚴格來說,需要對進行放縮以證明或者取出特殊點,同原題方法).所以在上單調遞增,在上單調遞減,在上單調遞增,而,所以,而在時可以取到負值,在時可以取到正數(仍然需要嚴格處理函數,同原題方法),所以此時一定有三個零點,所以的取值范圍是.
