08：00-24:00
很多同學問小數老師如何解選擇題，小數老師總結了一下，希望對大家有所幫助！
1.標準化試題的漏洞
除了用了知識點之外，用選擇題本身固有漏洞做題。大家記住一點，所有選擇題，題目或者答案必然存在做題暗示點。因為首先我們必須得承認，這題能做，只要題能做，必須要有暗示。
1）有選項。利用選項之間的關系，我們可以判斷答案是選或不選。如兩個選項意思完全相反，則必有正確答案。
2）答案只有一個。大家都有這個經驗，當時不明白什么道理，但是看到答案就能明白。由此選項將產生暗示
3）題目暗示。選擇題的題目必須得說清楚。大家在審題過程中，是必須要用到有效的訊息的，題目本身就給出了暗示。
4）利用干擾選項做題。選擇題除了正確答案外，其他的都是干擾選項，除非是亂出的選項，否則都是可以利用選項的干擾性做題。一般出題者不會隨意出個選項，總是和正確答案有點關系，或者是可能出錯的結果，我們就可以借助這個命題過程得出正確的結論。
5）選擇題只管結果，不管中間過程，因此在解題過程中可以大膽的簡化中間過程。
6）選擇題必須考察課本知識，做題過程中，可以判斷和課本哪個知識相關？那個選項與這個知識點無關的可立即排除。因此聯系課本知識點做題。
7）選項是最佳的（語言類考試），選項是比出來的。
8）選擇題必須保證考生在有限時間內可以做出來的，因此當大家花很多時間想不對的時候，說明思路錯了。選擇題必須是由一個簡單的思路構成的。
2.使用準則
平時訓練時也講到一些技巧，但是學生并不知道在什么情況下用什么技巧，因此這里給大家帶來的管衛東選擇題考試技術將明確的告訴大家，第一，技巧是什么，第二，什么狀態下用（要么第一遍做題的時候使用，或者做不下的時候用）。
先說什么時候用，大家平時做的熟的題、有把握能夠快速做出來的時候，就按照自己的方法做。如果沒思路、做不下去，或者發現做的時候需要大量計算的時候，可以明確的告訴自己，你的方向錯了，可以換一種思路了。
三、部分選擇題方法
1）數學選項暗示：
①開閉區間開閉區間的思想就是暗示我們能不能取到這個值，直接代入驗證就行。一般可通過數形結合來判斷其具體取值。
②含有+∞及-∞的。即極限討論法，一般有給出無窮大的選項，我么可用極限的思想去討論排除或者待選（案例較多，大家自行找任意題去驗證）。
③函數單調性判斷。根據單調性的特征取兩個到三個好算的特殊值驗證即可得出結論。
④函數奇偶性判斷。根據對稱特性，取相應的對稱點驗證是否成立。
例題：最新的北京西城一模理科第七題
7．設等比數列{an}的各項均為正數，公比為q，前n項和為Sn．若對n屬于正整數，，有S2n＜3Sn，則q的取值范圍是（）
A（0,1]B(0,2) C[1,2) D(0,√2)
本題就可以代入驗證和極限思維去解題。讓a1=1，然后直接猜答。
先比較S2n比較Sn，q的次方一定更多，故而q在（0,1]之間肯定滿足（遞增，q取1最大，那么S2n為2q，3Sn為3q），直接排除C選項。
而后直接采用極限思想，考慮q大于1，前者的次方是后者次方的2倍，我們不考慮求和，只思考單項，即q2n和3qn的大小即可，相除，得出qn除以3＜1，因為n可以取任意無限大，只要q＞1，故而這個式子就顯然不能恒成立，故而只能選擇A。
如果按照傳統做法，必須列表達式，即Sn=…… S2n=……，然后兩廂比較，討論各種情況，反而會出現越來越多的可能。而直接令a1=1，而后比較最終項，就能得出答案，何樂而不為呢。
2）根據所學知識點簡化
僅限數學，我們完全可以利用知識點干掉干擾條件，當你常規方法做不下去的時候，就這么做。
我們不必管其中的道理，但是這類題通常比較難，我們在完全沒有思路的時候，完全可以利用知識點來簡化，如下題：
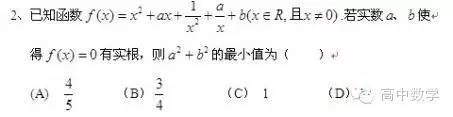
這道題估計很多人沒思路，或者埋頭計算了，其實根據課本知識點，因選擇題不考慮中間過程，我們完全可以將x給弄沒了，但是不能瞎弄沒。高中哪些知識點和求極值有關？第一是導數，第二是不等式，如果用導數是針對x的，我們求的是a和b，所以我們用不等式，發現若一、三項相乘，二、四項相乘，就剩下1和a的平方了，這個完全符合均值不等式，我們不必管為什么，那么在取等號f（x）=0的情況下，x=1/x，即x=1或x=-1，隨便取x=1或-1，就能得出2a+b+2=0，那么到這里就明白是求原點到直線的最小距離，也就是圓點到直線的垂線。因為是選擇題，并且躲不開課本，我們可以大膽的這么做。很多人不敢這么做，但是就用這么大膽去做這類題，你可以隨便找題來，表面看很冒險，但是卻可以達到100%的正確率。
3）定性理解做題法：數形結合
但凡考題涉及到函數和坐標系的，直接畫圖。 比如今年4月份海淀區模考試題：
很多人這道題不會做，而只要通過畫圖，可以迅速得出答案，基本上初中生都能答對。我們根據函數，一個是開口向下，對稱軸為a/2，只能取x≤1的二次函數，以及斜率為a，x＞1的直線。要求它們各取一點，y值相等即可，即這兩個點能夠處在同一水平線（平行x軸）
那么只要畫圖，就知道當x≤1時，必定會過x軸下方，而a小于0時，ax-1是過第四想象的，也必然會通過x軸下方，故而直接選A。如果不放心D選項，那么直接令a=3，代入即可，因為二次函數對稱軸為1.5，取不到，故而最大值是x=1，f（x）=2，而ax-1由于x＞1，故而ax-1的最小值大于2，故而沒有交點，所以排除。
4）特殊值
但凡題目給的字母沒有特別限制的，可去特殊值：
三角形之內必定去邊界值（0，1等），如果取一般值如45°、60°、30°、90°可以用來參照。這題大家自行代入即可得出結論，而不是去做式子變形，將能節約大量時間。
根據學生的高考分數、意向專業 為您查找適合你的院校列表， 24小時內短信電話發送給你！
