08：00-24:00
已知單位向量，且，設
，則的最大值是______．
分析與解法一根據題意，有
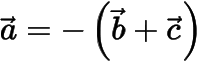
，于是可得
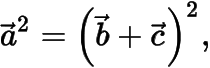
因此
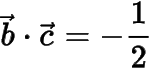
，類似的，可得
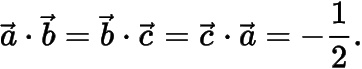
因此
是共面向量，且兩兩的夾角均為．設是與
均垂直的單位向量，且則此時
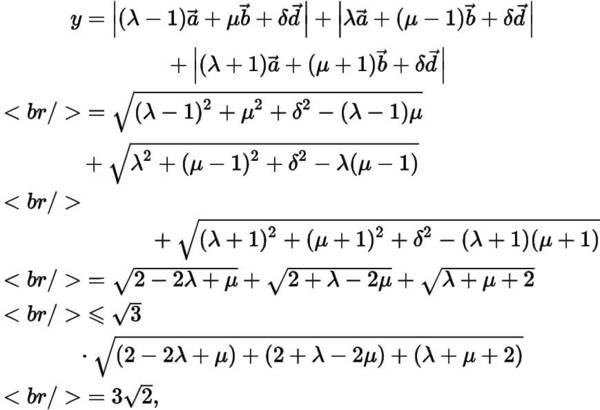
等號當時取得．因此所求的最大值為．
法二由柯西不等式，有
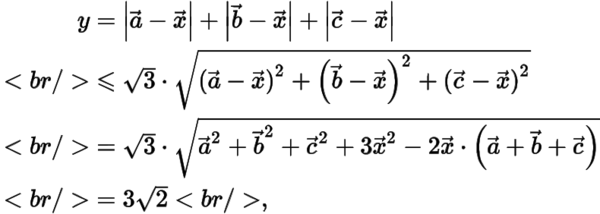
等號當
時取得．事實上，有
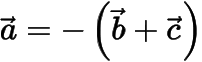
，于是可得
因此
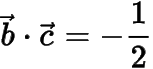
，類似的，可得
因此
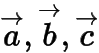
是共面向量，且兩兩的夾角均為．進而取與
均垂直，即可取得等號．因此所求的最大值為．
注如果限定所有向量為平面向量，也可對應的兩種方法：
法一此時，于是且．不妨設，則不難證明
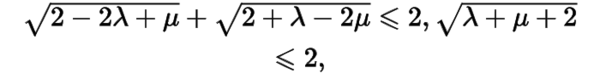
等號當時同時取得，因此此時所求的最大值為．
注事實上，有
法二設，，，，且不妨設落在劣弧上(包括端點)，那么等號當為外接圓的直徑，即時取得．因此所求的最大值為．
注事實上，有，由托勒密定理或者平面幾何的知識可以證明．
根據學生的高考分數、意向專業(yè) 為您查找適合你的院校列表， 24小時內短信電話發(fā)送給你！
