08：00-24:00
已知橢圓
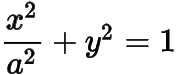
的離心率為
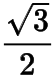
，為圓上任意一點(diǎn)，過作橢圓的兩條切線．設(shè)切點(diǎn)分別為．
(1) 證明：切線的方程為
；
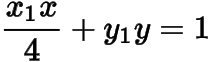
(2) 設(shè)為坐標(biāo)原點(diǎn)，求面積的最大值．
分析與解(1) 橢圓的方程為
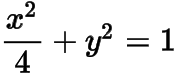
．設(shè)點(diǎn)的方程為
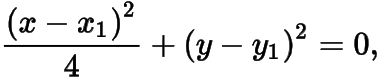
利用交點(diǎn)曲線系可得切線的方程為
整理得
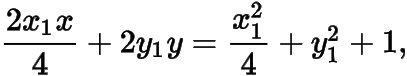
由于
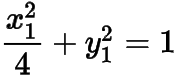
，可得
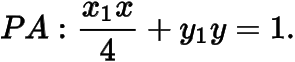
(2) 作仿射變換，，則問題等價于從橢圓
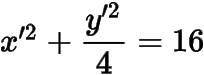
上點(diǎn)引圓的兩條切線，切點(diǎn)分別為，求的面積的最大值的一半．的面積只與有關(guān)，設(shè)()，則
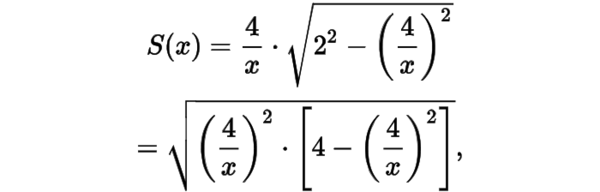
由于
的取值范圍是
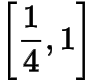
，于是的取值范圍是
，其最大值為．回到原問題，所求的面積的最大值為
．
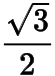
注由曲線系得到的方程是過點(diǎn)的直線，且橢圓上不存在另外一個點(diǎn)也在此直線上，所以它是切線的方程．
根據(jù)學(xué)生的高考分?jǐn)?shù)、意向?qū)I(yè) 為您查找適合你的院校列表， 24小時內(nèi)短信電話發(fā)送給你！
版權(quán)所有：中教未來（北京）文化傳播有限公司 Copyright(c)2001-2025 rights reserved m.3848080.com 京ICP備14025495號-5
高校特色專業(yè)招生咨詢熱線：4007-567-088
